نظرية فيرما في الرياضيات

تُعرف معضلة فيرما أو نظرية فيرما الأخيرة (Fermat’s Last Theorem) بأنها واحدة من أعمق وأشهر المعضلات الرياضية التي شغلت العلماء لأكثر من ثلاثة قرون.

وقد وضع العالم الفرنسي بيير دي فيرما (Pierre de Fermat) هذه النظرية في القرن السابع عشر كتعليق في هامش كتابٍ، وأثار تحديًا عظيمًا في الأوساط الرياضية لمئات السنين.

صياغة نظرية فيرما الأخيرة

تنص نظرية فيرما على أنه “لا توجد أي مجموعة من الأعداد الصحيحة \(x\)، و\(y\)، و\(z\) تفي بالمعادلة التالية، إذا كانت \(n\) عددًا صحيحًا أكبر من 2”:

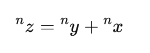
هذه الصياغة البسيطة خدعت الكثيرين، إذ تبدو كأنها مسألة رياضية مباشرة، لكن اتضح أنها أكثر تعقيدًا مما كان يعتقد فيرما نفسه.

محاولات إثبات النظرية عبر القرون

بعد كتابة فيرما لهذه النظرية، لم يقدم أي دليل عليها، مما جعلها تحديًا كبيرًا للرياضيين في جميع أنحاء العالم.

وبمرور الوقت، حاول العديد من العلماء إثبات النظرية باستخدام تقنيات رياضية متنوعة، إلا أن أيًا منهم لم يتمكن من الوصول إلى حل نهائي.

في القرن العشرين، وبالتحديد في الثمانينيات، بدأت المحاولات الجادة نحو إثبات النظرية باستخدام أساليب متقدمة مثل نظرية الأعداد الجبرية (Algebraic Number Theory) والهندسة الجبرية (Algebraic Geometry).

إثبات أندرو وايلز

في عام 1994، تمكن العالم البريطاني أندرو وايلز (Andrew Wiles) من إثبات نظرية فيرما الأخيرة باستخدام تقنيات رياضية معقدة.

اعتمد وايلز على نظرية الحزم الجبرية (Elliptic Curves) ونظرية الأعداد.

قام بإثبات النظرية عن طريق ربط معضلة فيرما بأحد أكبر مشاكل الرياضيات آنذاك، والمعروفة بـ”حدسية تانياما-شيمورا” (Taniyama-Shimura Conjecture).

أهمية إثبات وايلز

حقق إثبات وايلز نجاحًا باهرًا في المجتمع الرياضي، ليس فقط لإثباته معضلة رياضية كانت قائمة لأكثر من 350 سنة، ولكن أيضًا لأنه أدخل طرقًا وأساليب جديدة إلى نظرية الأعداد (Number Theory) والهندسة الجبرية.

ويمكن القول بأن هذا الإنجاز قد ساهم في تطوير مجالات رياضية واسعة، وقد فاز وايلز بالعديد من الجوائز تقديرًا لعمله.

تأثير نظرية فيرما على الرياضيات الحديثة

لم تقتصر أهمية نظرية فيرما على كونها تحديًا رياضيًا فحسب، بل إنها أثرت بشكل كبير على مجالات متعددة مثل التحليل المعقد (Complex Analysis) ونظرية الزمر (Group Theory).

فقد ألهمت النظرية أجيالًا من الرياضيين لاكتشاف علاقات جديدة وابتكار طرق مبتكرة لإثبات النظريات.

تمثل نظرية فيرما الأخيرة مثالًا رائعًا على كيفية أن تتحدى مسألة بسيطة نسبيًا عقول الرياضيين لعقود.

لقد أظهر إثبات وايلز أن الإرادة والتفاني في السعي وراء الحقيقة يمكن أن يؤديان إلى اكتشافات عميقة تؤثر على العلوم بأكملها.